Question

The height of a helicopter above the ground is given by h = 3.15t3, where h is in meters and t is in seconds. At t = 2.10 s, the helicopter releases a small mailbag.

How long after its release does the mailbag reach the ground?

Answer 1

The mailbag will take 2.44 seconds to reach the ground.

Step-by-step explanation:

The height of a helicopter above the ground is given by:

`h = 3.15* t^3`

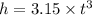
Height of helicopter at t = 2.10 seconds

`h(2.10 )=3.15* (2.10 )^3 m=29.17 m`

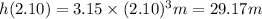
The helicopter releases a small mailbag from the height of 29.17 m.

The initial velocity of mailbag = u = 0 m/s

Duration in which mailbag will reach the ground = T

Acceleration due to gravity = g =
`9.8 m/s^2`

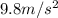
Using second equation of motion ;

`s=ut+(1)/(2)gt^2`

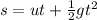
We have , s = 29.17

u = 0 m/s

t = T

`29.17m=0 m/s* T+(9.8 m/s^2* T^2)/(2)`

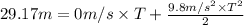
Solving for T, we gte :

T = 2.44 seconds

The mailbag will take 2.44 seconds to reach the ground.