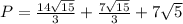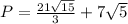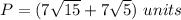Answer:
Explanation:
see the attached figure to better understand the problem
step 1
Find the length side AB (hypotenuse)
we know that
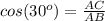
substitute
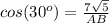
Remember that

so
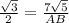
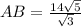
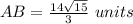
step 2
Find the length side BC
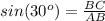

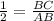
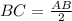
substitute the value of AB
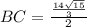
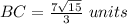
step 3
Find the perimeter
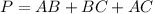
substitute