Question

What are the zeros of f(x) = x2 + x - 30?

Ο
A. X = -5 and x = 6
B. X = -6 and x = 5
Ο.
O
C. x = -2 and x = 15
O
D. x = -15 and x = 2

Answer 1

Therefore the zeros of

`f(x)=x^(2)+x-30`

are

`x=-6\ and\ x= 5`

Explanation:

Given:

`f(x)=x^(2)+x-30`

To Find:

Zeros of the function.

Solution:

Zeros of Polynomial or function:

Zeros of the polynomial means while substituting the value of X in the polynomial you will get the value of the polynomial or function equals to Zero.

Hence to find a value of zeros , the value of function should be zero.

Therefore,

f(x) =0

`x^(2)+x-30=0`

To find the value of 'x' we need to factorize the above quadratic equation.

First is to remove the factor of -30 such that when you add the factors you should get one.

-30 = 6 × -5

6 - 5 = 1

Hence by splitting the middle term we get

`x^(2)+6x-5x-30=0\\x(x+6)-5(x+6)=0\\(x+6)(x-5)=0\\x+6=0\ or\ x-5=0\\x=-6\ or\ x=5`

Therefore the zeros of

`f(x)=x^(2)+x-30`

are

`x=-6\ and\ x= 5`

Answer 2

the zeros as x = 5 or x = -6 . SO the correct option is Option B.

Explanation:

i) the zeros of any expression of f(x) is found by equating f(x) to zero and then solving for x.

ii) therefore to find the zeros ( or roots) of the given expression we can write f(x) =
`x^(2) + x - 30 = 0`

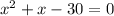
iii) therefore
`x^(2) + x - 30 = 0` ⇒
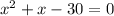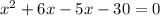`x^(2) + 6x - 5x - 30 = 0` .... from visual observation

therefore we can write
`x( x + 6) -5(x + 6) = 0` ⇒
`(x - 5)(x + 6) = 0`

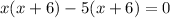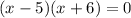
therefore either x - 5 = 0, or, x + 6 = 0 if the above equation is to be true.

iv) therefore solving for x we get the zeros as x = 5 or x = -6. So the correct option is Option B.