Answer:
The time difference is 8.33 ms.
The phase difference between them is 60°
Step-by-step explanation:
Given that,
Frequency = 10 Hz
Angle = 30°
We need to calculate the time difference
Using formula of time difference
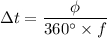
Put the value into the formula
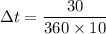
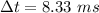
If the frequency of these sine waves doubles, but the time difference stays the same,
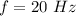
We need to calculate the phase difference between them
Using formula of phase difference
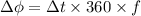
Put the value in to the formula
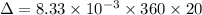
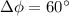
Hence, The time difference is 8.33 ms.
The phase difference between them is 60°