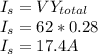Question

The real power delivered by a source to two impedances, ????1=4+????5⁡Ω and ????2=10⁡Ω connected in parallel, is 1000 W. Determine (a) the real power absorbed by each of the impedances and (b) the source current.

Answer 1

The question is incomplete, below is the complete question

"The real power delivered by a source to two impedance, Z1=4+j5⁡Ω and Z2=10⁡Ω connected in parallel, is 1000 W. Determine (a) the real power absorbed by each of the impedances and (b) the source current."

answer:

a. 615W, 384.4W

b. 17.4A

Step-by-step explanation:

To determine the real power absorbed by the impedance, we need to find first the equivalent admittance for each impedance.

recall that the symbol for admittance is Y and express as

`Y=(1)/(Z)`

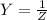
Hence for each we have,

`Y_(1) =1/Zx_(1)\\Y_(1) =(1)/(4+j5)\\converting to polar \\ Y_(1) =(1)/(6.4\leq 51.3)\\ Y_(1) =(0.16 \leq -51.3)S`

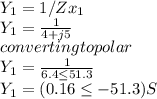
for the second impedance we have

`Y_(2)=(1)/(10)\\Y_(2)=0.1S`

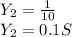
we also determine the voltage cross the impedance,

P=V^2(Y1 +Y2)

`V=\sqrt{(P)/(Y_(1)+Y_(2))}\\`

`V=\sqrt{(1000)/(0.16+0.1)}\\ V=62v`

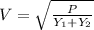
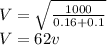
The real power in the impedance is calculated as

`P_(1)=v^(2)G_(1)\\P_(1)=62*62*0.16\\ P_(1)=615W`

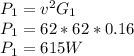
for the second impedance

`P_(2)=v^(2)*G_(2)\\ P_(2)=62*62*0.1\\384.4w`

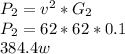
b. We determine the equivalent admittance

`Y_(total)=Y_(1)+Y_(2)\\Y_(total)=(0.16\leq -51.3 )+0.1\\Y_(total)=(0.16-j1.0)+0.1\\Y_(total)=0.26-J1.0\\`

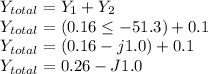
We convert the equivalent admittance back into the polar form

`Y_(total)=0.28\leq -19.65\\`

the source current flows is

`I_(s)=VY_(total)\\I_(s)=62*0.28\\I_(s)=17.4A`