Question

Produce an infinite collection of sets A1, A2... with the property that every Ai has an infinite number pf elements , Ai inter Aj = empty set for all i, j different.

and Uinfinitii=1Ai =N

Answer 1

`A_n = [2^(n-1) , 3(2^(n-1)), 5(2^(n-1)), 7(2^(n-1)),....]`

Explanation:

For this case we need to produce an infinite collection of sets
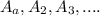`A_a, A_2, A_3,....` with the property that every
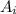`A_i` has an infinite number of elements with
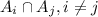`A_i \cap A_j , i\\eq j` and
`\cup_(i=1)^(\infty) A_i = N`

So for this case we need to create a set A who satisfy 3 conditions (Infinite number of elements, Disjoint and Union represent the natural numbers)

So if we define the nth term for the set A:

`A_n = [2^(n-1) , 3(2^(n-1)), 5(2^(n-1)), 7(2^(n-1)),....]`

We see that the set A represent all the odd multiplies of
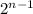`2^(n-1)` and if we check the properties we have this:

Disjoint

If we select
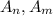`A_n , A_m` with
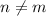`n\\eq m` and we can assume for example that
`n<m` and if we have an element a in the intersection of the sets
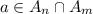`a \in A_n \cap A_m`, so then needs to exists some odd numbers k and l such that

`a = 2^(n-1) k = 2^(m-1)l`

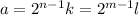
And since we assume that
`n<m` then we have that
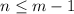`n\leq m-1` and we can write:

`2^(m-1) =2^m 2^i , i\geq 0`

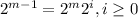
And then
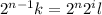`2^(n-1) k= 2^n 2^i l` and if we divide by
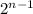`2^(n-1)` we got:

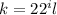`k = 2 2^i l` so then k is not odd since the last statement contradicts this. So then we can conclude that
`A_n \cap A_m = \emptyset`

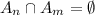
Union

For this case we need to show that
`\cup_(i=1)^(\infty) A_i = N`

Since each element
`A_n` is a subset of the natural numbers then the unision of the sets represent N

For the other side of the explanation if we assume that
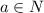`a\in N` we can write
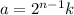`a= 2^(n-1)k` for any
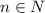`n\in N` and k odd, and by this
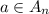`a\in A_n` and we chaek the property.

Infinite condition

For this case
`A_n = [2^(n-1) , 3(2^(n-1)), 5(2^(n-1)), 7(2^(n-1)),....]`

is an infinite set since we don't have a limit for n so then we have infinite elements for this case.

And since all the properties are satisfied we end the problem.