Question

Assume that 1200 births are randomly selected and exactly 608 of the births are girls. Use subjective judgment to determine whether the given outcome is unlikely, and also determine whether it is unusual in the sense that the result is far from what is typically expected.

a. Determine whether exactly 608 girls out of 1200 randomly selected births is unlikely.
b. Determine whether exactly 608 girls out of 1200 randomly selected births is unusual.

Answer 1

a) For this case we have just one possibility out of 1200 births, since the other possiblities for the number of girls in 1200 are {1,2,3,......,607,609,610,.....,1200}, so then the probability for 698 is just :

`p=(1)/(1200)=0.000833`

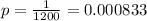
And since the probability is <0.05 we can consider the event unlikely.

b) If the number observed is similar than the expected value we can consider the event not unusual.

The expected value for this case since we have a sample 1200 and assuming the probability of being girl 0.5 then the expected value would be:

`E(X) = n*p = 1200*0.5 = 600`

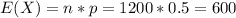
So as we can see 608 is not far away from the expected value so then we can consider the event NOT unusual

Step-by-step explanation:

For this case we need to remember that an event is unlikely if the probability is very small for example <0.05. The complement for the event would be the probability for how likely is.

For this case we have the following event: A="In 1200 births selected exactly 698 of the births are girls"

Part a

For this case we have just one possibility out of 1200 births, since the other possiblities for the number of girls in 1200 are {1,2,3,......,607,609,610,.....,1200}, so then the probability for 698 is just :

`p=(1)/(1200)=0.000833`

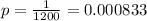
And since the probability is <0.05 we can consider the event unlikely.

Part b

If the number observed is similar than the expected value we can consider the event not unusual.

The expected value for this case since we have a sample 1200 and assuming the probability of being girl 0.5 then the expected value would be:

`E(X) = n*p = 1200*0.5 = 600`

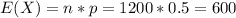
So as we can see 608 is not far way from the expected value so then we can consider the event NOT unusual