Answer:
n=0.03928 moles
Moles of oxygen do the lungs contain at the end of an inflation are 0.03928 moles
Step-by-step explanation:
The amount of oxygen which lung can have is 20% of 5 L which is the capacity of lungs
Volume of oxygen in lungs =V=5*20%= 1 L=
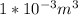
Temperature=T=
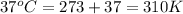
Pressure at sea level = P= 1 atm=

R is universal Gas Constant =8.314 J/mol.K
Formula:
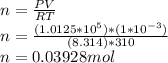
Moles of oxygen do the lungs contain at the end of an inflation are 0.03928 moles