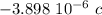Answer:
The initial charges on the spheres are
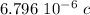 and
and
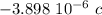
Step-by-step explanation:
Electrostatic Force
Two charges q1 and q2 separated a distance d exert a force on each other which magnitude is computed by the known Coulomb's formula
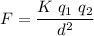
We are given the distance between two unknown charges d=50 cm = 0.5 m and the attractive force of -0.9537 N. This means both charges are opposite signs.
With these conditions we set the equation
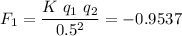
Rearranging
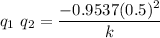
Solving for q1.q2
![\displaystyle q_1\ q_2=-2.6492.10^(-11)\ c^2\ \ ......[1]](https://img.qammunity.org/2021/formulas/physics/college/5wy18or1ujs8y2vsn1cuc9trgxgs9a2qwp.png)
The second part of the problem states the spheres are later connected by a conducting wire which is removed, and then, the spheres repel each other with an electrostatic force of 0.0756 N.
The conducting wire makes the charges on both spheres to balance, i.e. free electrons of the negative charge pass to the positive charge and they finally have the same charge:
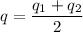
Using this second condition:
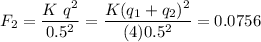
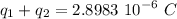
Solving for q2
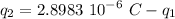
Replacing in [1]
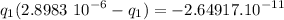
Rearranging, we have a second-degree equation for q1.
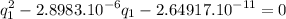
Solving, we have two possible solutions
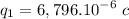
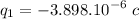
Which yields to two solutions for q2
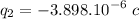
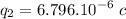
Regardless of their order, the initial charges on the spheres are
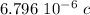 and
and