Answer:
a)

b)
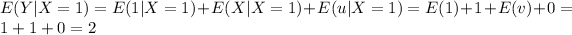
c)
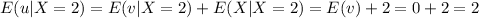
d)
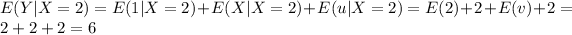
e)
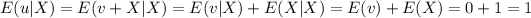
f)
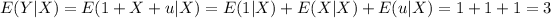
g)
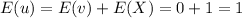
h) E(Y) = E(1+X+u) = E(1) + E(X) +E(v+X) = 1+1 + E(v) +E(X) = 1+1+0+1 = 3[/tex]
Explanation:
For this case we know this:
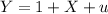
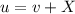
with both Y and u random variables, we also know that:
![[tex] E(v) = 0, Var(v) =1, E(X) = 1, Var(X)=2](https://img.qammunity.org/2021/formulas/mathematics/college/spmqsw0npkm72908asztppbbrto3vkquhp.png)
And we want to calculate this:
Part a
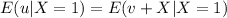
Using properties for the conditional expected value we have this:
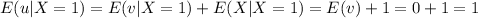
Because we assume that v and X are independent
Part b
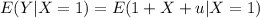
If we distribute the expected value we got:
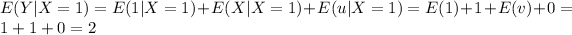
Part c
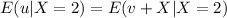
Using properties for the conditional expected value we have this:
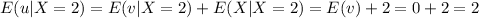
Because we assume that v and X are independent
Part d
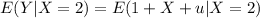
If we distribute the expected value we got:
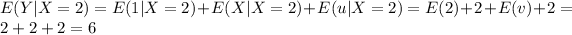
Part e
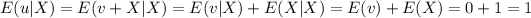
Part f
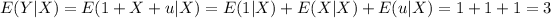
Part g
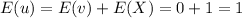
Part h
E(Y) = E(1+X+u) = E(1) + E(X) +E(v+X) = 1+1 + E(v) +E(X) = 1+1+0+1 = 3[/tex]