Answer: The pH of the solution is 4.57
Step-by-step explanation:
To calculate the number of moles for given molarity, we use the equation:
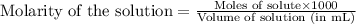
Molarity of benzoic acid = 50 mM = 0.05 M (Conversion factor: 1 M = 1000 mM)
Volume of solution = 100 mL
Putting values in above equation, we get:
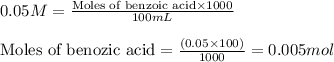
Molarity of sodium hydroxide = 50 mM = 0.05 M
Volume of solution = 70 mL
Putting values in above equation, we get:
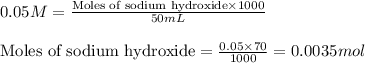
The chemical reaction for sodium hydroxide and benzoic acid follows the equation:
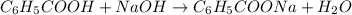
Initial: 0.005 0.0035
Final: 0.0015 - 0.0035
Volume of solution = 100 + 70 = 170 mL = 0.170 L (Conversion factor: 1 L = 1000 mL)
To calculate the pH of acidic buffer, we use the equation given by Henderson Hasselbalch:
![pH=pK_a+\log(([salt])/([acid]))](https://img.qammunity.org/2021/formulas/biology/college/6usxe642bp3w274zbcv30her0kcessu95f.png)
![pH=pK_a+\log(([C_6H_5COONa])/([C_6H_5COOH]))](https://img.qammunity.org/2021/formulas/chemistry/college/56bssrwayoflafen4p2r9657nyn9ht5fxf.png)
We are given:
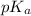 = negative logarithm of acid dissociation constant of benzoic acid = 4.2
= negative logarithm of acid dissociation constant of benzoic acid = 4.2
![[C_6H_5COONa]=(0.0035)/(0.170)](https://img.qammunity.org/2021/formulas/chemistry/college/l2rakaof9y2rv28ozk82rir78zwbgk8c9j.png)
![[C_6H_5COOH]=(0.0015)/(0.170)](https://img.qammunity.org/2021/formulas/chemistry/college/s9s327k1r7b0vmfs3h8e0nmd8r20uvflw4.png)
pH = ?
Putting values in above equation, we get:
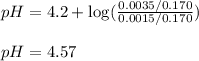
Hence, the pH of the solution is 4.57