Question

The equation r(t)=cos(5t)i + sin(5t)j, 0t≥0 describes the motion of a particle moving along the unit circle. Answer the following questions about the behavior of the particle. a. Does the particle have constant​ speed? If​ so, what is its constant​ speed? b. Is the​ particle's acceleration vector always orthogonal to its velocity​ vector? c. Does the particle move clockwise or counterclockwise around the​ circle? d. Does the particle begin at the point left parenthesis 1 comma 0 right parenthesis(1,0)​?

Answer 1

a) 5 units/s

b) yes

c) counter-clockwise

d) yes

Explanation:

part a

r(t) = cos (5t) i + sin (5t)j

v(t) = dr(t) / dt = -5sin(5t) i + 5cos(5t)j

`mag( v(t)) = √((-5sin(5t))^2 + (5cos(5t))^2) \\mag( v(t)) = √(25sin^2(5t) + 25cos^2(5t)) \\ \\mag( v(t)) = √(25*(sin(5t)^2 + cos(5t)^2)) \\\\mag( v(t)) = √(25) \\\\mag( v(t)) = 5 units/s`

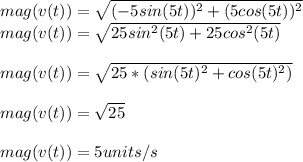
Hence, the particle has a constant speed of 5 units/s

part b

a(t) = dv(t) / dt = -25cos(5t) i - 25sin(5t)j

To check orthogonality of two vectors their dot product must be zero

a(t) . v(t) = (-25cos(5t) i - 25sin(5t)j) . (-5sin(5t) i + 5cos(5t)j)

= 125cos(5t)*sin(5t) -125cos(5t)*sin(5t)

= 0

Yes, the particles velocity vector is always orthogonal to acceleration vector.

part c

Use any two values of t and compute results of r(t)

t = 0 , r(0) = 1 i

t = pi/2, r(0) = j

Hence we can see that the particle moves counter-clockwise

part d

Find the value r(t) at t=0

r(0) = cos (0) i + sin (0) j

r(0) = 1 i + 0 j

Yes, the particle starts at point ( 1, 0)