Question

I wish to determine the correlation between the height (in inches) and weight (in pounds) of 21-year-old males. To do this, I measure the height and weight of two 21-year-old men. The measured values are Height and weight of male 1: 70, 169 Height and weight of male 2: 69,164 The correlation r computed from the measurements on these males is Question 2 options: 1.0 -1.0 near 0 because the heights and weights of the men are similar.

Answer 1

`r=(2(23146)-(139)(333))/(√([2(9661) -(139)^2][2(55457) -(333)^2]))=1`

So then the we have perfect linear association. Because the heights and weights of the men are similar.

Explanation:

Let X represent the Height and Y the weigth

We have the follwoing dataset:

X: 70, 69

Y: 169, 164

n=2

The correlation coefficient is a "statistical measure that calculates the strength of the relationship between the relative movements of two variables". It's denoted by r and its always between -1 and 1.

And in order to calculate the correlation coefficient we can use this formula:

`r=(n(\sum xy)-(\sum x)(\sum y))/(√([n\sum x^2 -(\sum x)^2][n\sum y^2 -(\sum y)^2]))`

For our case we have this:

n=2
`\sum x = 139, \sum y = 333, \sum xy = 23146, \sum x^2 =9661, \sum y^2 =55457`

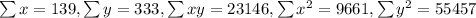
And if we replace in the formula we got:

`r=(2(23146)-(139)(333))/(√([2(9661) -(139)^2][2(55457) -(333)^2]))=1`

So then the we have perfect linear association. Because the heights and weights of the men are similar.