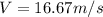Question

When the ambulance passes the person (switching from moving towards him to moving away from him), the perceived frequency of the sound he receives decreases by 9.27 percent. How fast is the ambulance driving?

Answer 1

To develop this problem we will apply the considerations made through the concept of Doppler effect. The Doppler effect is the change in the perceived frequency of any wave movement when the emitter, or focus of waves, and the receiver, or observer, move relative to each other. At first the source is moving towards the observer. Than the perceived frequency at first

`F_1 = F \frac{{343}}{(343-V)}`

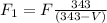
Where F is the actual frequency and v is the velocity of the ambulance

Now the source is moving away from the observer.

`F_2 = F(343)/((343+V))`

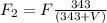
We are also so told the perceived frequency decreases by 11.9%

`F_2 = F_1 - 9.27\% \text{ of } F_1`

`F_2 = F_1-0.0927F_1`

`F_2 = 0.9073F_1`

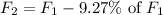
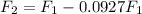
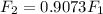
Equating,

`F(343)/((343+V))= 0.9073(F(343)/((343-V)))`

`(1)/((343+V))= 0.9073(1)/((343-V))`

`0.9073(343+V) = 343-V`

`(0.9073)(343)+(0.9073)V = 343-V`

`V+0.9073V = 343-(0.9073)(343)`

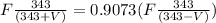
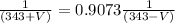
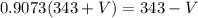
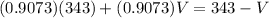
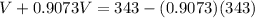
Solving for V,

`V = 16.67 m/s`