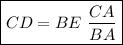Question

If we want to find the height of an object like a flagpole, we can use triangles. In the graphic above, triangle ABE is similar to triangle ACD. In the graphic line segment DC is the height of the . Using the length of BE (your height), AB (your shadow), and AC (the shadow of flagpole), we can use a proportion to determine the height of the .

Answer 1

Answer:If we want to find the height of an object like a flagpole, we can use right triangles. In the graphic above, triangle ABE is similar to triangle ACD. In the graphic line segment DC is the height of the flagpole. Using the length of BE (your height), AB (your shadow), and AC (the shadow of flagpole), we can use a proportion to determine the height of the flagpole.

Explanation: fill in the blank

Answer 2

`\displaystyle CD=BE\ (CA)/(BA)`

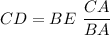
Step-by-step explanation:

Thales Theorem

It applies when a line is drawn parallel to one side of a triangle and it intersects the other two sides. The theorem states that line divides the two sides in the same ratio or proportion.

We have drawn the triangle that describes the situation stated in the question, where we want to know the value of CD, knowing the values of BE, BA, and CA. The red line BE is parallel to the line CD, so the Tales theorem must stand meaning that the sides AC and AB are proportionally divided at the same ratio as CD and BA, thus

`\displaystyle (CD)/(BE)=(CA)/(BA)`

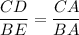
We can solve for CD (the height of the flagpole)

`\boxed{\displaystyle CD=BE\ (CA)/(BA)}`