Question

Sociologists want to determine the probability of exactly 4 out of the next 7 individuals they survey earning over

$50,000 dollars per year. The probability of an individual earning over $50,000 a year is 30%. What is the probability of
exactly 4 out of the next 7 individuals that they survey earning over $50,000?
A. 0.07859
B. 0.07651
C. 0.08311
D. 0.09724

Answer 1

the probability of exactly 4 out of next 7 individuals that the sociologists survey earning over $50000 is given by

=
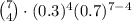`\binom{7}{4} \cdot (0.3)^4(0.7)^(7-4)` = 0.09724

Explanation:

i) This problem is solved by using the Binomial Probability distribution as the sample size is less than 30.

ii) The sample size is 7

iii) It is given that the probability of an individual earning over $50000 is 30% or 0.3 and therefore the probability of an individual not earning over $50000 is ( 1 - 0.3) = 0.7

iv) Therefore the probability of exactly 4 out of next 7 individuals that the sociologists survey earning over $50000 is given by

=
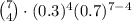`\binom{7}{4} \cdot (0.3)^4(0.7)^(7-4)` = 0.09724