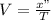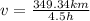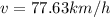Question

You are driving home from school steadily at 95 km/h for 180 km. It then begins to rain and you slow to 65 km/h. You arrive home after driving for 4.5 h. a. how far is your hometown from school?b. what was your average speed?

Answer 1

To solve this problem we will apply the linear motion kinematic equations, for this purpose we will define the time of each of the sections in which the speed is different. After determining the segments of these speeds we can calculate the average distance and the average speed. Our values are given as

x = 180 km

v = 95 km / h

Speed can be described as the displacement of a body per unit of time, and from that definition clearing the time we would have

`v = (x)/(t) \rightarrow t = (x)/(v)`

`v = (180)/(95)`

`v = 1.89473 hrs`

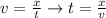
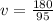
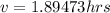
From the statement we have that the total time is 4.5, then he remaining time is

`t' = T-t =4.5-1.89473 = 2.60526 hrs`

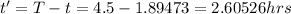
When it starts to rain there is a phase change in the speed which is given by

`v' = 65km/h`

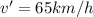
Then the distance travel in this velocity

`x' = v ' t '`

`x' = 65*2.60526`

`x = 169.34 km`

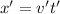
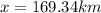
(a). Distance of your hometown from school ,

`x`

`x'' = 180+169.34`

`x= 349.34 km`

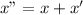
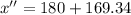
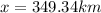
(b) The average speed

`V = (x`

`v = (349.34 km)/(4.5 h)`

`v = 77.63 km/ h`