Question

if (ax+2)(bx+7) = 15xsquared + cx +14 for all values of x, and a+b =8, what are the two possible values for c?

Answer 1

The two possible values for c are 31 and 41

Explanation:

Given Expression:

`(a x+2)(b x+7)=15 x^(2)+c x+14`

a + b = 8

To expand,

Multiply a x with (b x + 7) =
`a b x^(2)+7 a x`

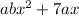
Multiply 2 with (b x + 7) = 2 b x +14

Now, combining the above, we get

`a b x^(2)+7 a x+2 b x+14=15 x^(2)+c x+14`

`a b x^(2)+x(7 a+2 b)+14=a b x^(2)`

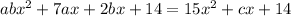
When comparing both sides, we get

a b = 15, 7 a + 2 b = c

`a=(15)/(b) \text { or } b=(a)/(15)`

Now, substitute above value in a + b = 8. So,

`(15)/(b)+b=8`

`15+b^(2)=8 b`

`b^(2)-8 b+15=0`

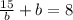
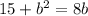
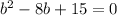
Factorising above, we get the equation as

`b^(2)-3 b-5 b+15=0`

(b - 3) (b - 5) = 0

b = 3 and 5

If b = 3, then

`a=(15)/(b)=(15)/(3)=5`

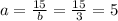
If b = 5, then

`a=(15)/(5)=3`

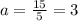
If a = 3, b = 5

c =7 a + 2 b = 7 (3) + 2 (5) = 21 + 10 = 31

If a = 5, b = 3

c =7 (5) +2 (3) = 35 + 6 = 41

Therefore, the values of ‘c’ are 31 and 41 .