Question

You're driving down the highway late one night at 20 m/s when a deer steps onto the road 38 m in front of you. Your reaction time before stepping on the brakes is 0.50 s , and the maximum deceleration of your car is 10 m/s2 .A. How much distance is between you and the deer when you come to a stop?

B. What is the maximum speed you could have and still not hit the deer?

Answer 1

given,

speed of the car = 20 m/s

final speed of car = 0 m/s

distance between car and the deer = 38 m

reaction time, t = 0.5 s

deceleration of the car = 10 m/s².

a) distance between deer and car

distance travel in the reaction time

d₁ = v x t

d₁ = 20 x 0.5 = 10 m

distance travel after you apply brake

using equation of motion

v² = u² + 2 a s

0 = 20² - 2 x 10 x s

s = 20 m

total distance traveled by the car

D = d₁ + d₂

D = 20 + 10 = 30 m

distance between car and the deer = 38 m - 30 m

= 8 m

b) now, maximum speed car.

distance travel in reaction time

d₁ = s x t

d₁ = 0.5 V

distance left between them

d₂ = 38 - d₁

d₂ = 38 - 0.5 V

distance travel after you apply brake

using equation of motion

v² = u² + 2 a d₂

0 = (V)² - 2 x 10 x (38 - 0.5 V)

V² + 10 V - 760 = 0

now, solving the quadratic equation

`x = (-b\pm √(b^2-4ac))/(2a)`

`V = (-10\pm √(10^2-4(1)(-760)))/(2(1))`

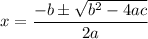
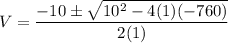
V = 23.01 , -33.01

rejecting the negative term.

hence, maximum speed of the car could be V = 23.01 m/s