Answer:
E (Y) = 3
Explanation:
If a 4-sided die is being rolled repeatedly; and the odd-numbered rolls (1st 3rd,5th, etc.)
The probability of odd number roll will be, p(T) =

However, on your even-numbered rolls, you are victorious if you get a 3 or 4. Also, the probability of even number roll, p(U) =

In order to calculate: E (Y); We can say Y to be the number of times you roll.
We know that;
E (Y) = E ( Y|T ) p(T) + E ( Y|U ) p(U)
Let us calculate E ( Y|T ) and E ( Y|U )
Y|T ≅ geometric =

Y|U ≅ geometric =

also; x ≅ geometric (p)
∴ E (x) =

⇒
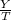 = 4 ; also
= 4 ; also
 = 2
= 2
E (Y) = 4 ×
 + 2 ×
+ 2 ×
= 2+1
E (Y) = 3