Question

Suppose the radius of the sphere is increasing at a constant rate of 0.3 centimeters per second. At the moment when the radius is 24 centimeters, the volume is increasing at a rate of?

Answer 1

At the moment when the radius is 24 centimeters, the volume is increasing at a rate of 2171.47 cm³/min.

Explanation:

We have equation for volume of a sphere

`V=(4)/(3)\pi r^3`

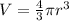
where r is the radius

Differentiating with respect to time,

`(dV)/(dt)=(d)/(dt)\left ((4)/(3)\pi r^3 \right )\\\\(dV)/(dt)=(4)/(3)\pi * 3r^2* (dr)/(dt)\\\\(dV)/(dt)=4\pi r^2* (dr)/(dt)`

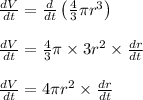
Given that

Radius, r = 24 cm

`(dr)/(dt)=0.3cm/s`

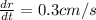
Substituting

`(dV)/(dt)=4\pi r^2* (dr)/(dt)\\\\(dV)/(dt)=4\pi * 24^2* 0.3\\\\(dV)/(dt)=2171.47cm^3/min`

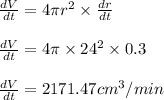
At the moment when the radius is 24 centimeters, the volume is increasing at a rate of 2171.47 cm³/min.