Question

Simplify this please​

Answer 1

`\frac{12q^{(7)/(3)}}{p^(3)}`

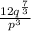
Explanation:

Here are some rules you need to simplify this expression:

Distribute exponents: When you raise an exponent to another exponent, you multiply the exponents together. This includes exponents that are fractions.
`(a^(x))^(n) = a^(xn)`

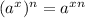
Negative exponent rule: When an exponent is negative, you can make it positive by making the base a fraction. When the number is apart of a bigger fraction, you can move it to the other side (top/bottom).
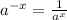`a^(-x) = (1)/(a^(x))`, and to help with this question:
`(a^(-x)b)/(1) = (b)/(a^(x))`.

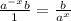Multiplying exponents with same base: When exponential numbers have the same base, you can combine them by adding their exponents together.
`(a^(x))(a^(y)) = a^(x+y)`

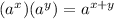
Dividing exponents with same base: When exponential numbers have the same base, you can combine them by subtracting the exponents.
`(a^(x))/(a^(y)) = a^(x-y)`

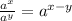
Fractional exponents as a radical: When a number has an exponent that is a fraction, the numerator can remain the exponent, and the denominator becomes the index (example, index here ∛ is 3).
`a^{(m)/(n)} = \sqrt[n]{a^(m)} = (\sqrt[n]{a})^(m)`

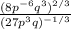`((8p^(-6) q^(3))^(2/3))/((27p^(3)q)^(-1/3))` Distribute exponent

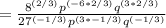`=(8^((2/3))p^((-6*2/3))q^((3*2/3)))/(27^((-1/3))p^((3*-1/3))q^((-1/3)))` Simplify each exponent by multiplying

`=(8^((2/3))p^((-4))q^((2)))/(27^((-1/3))p^((-1))q^((-1/3)))` Negative exponent rule

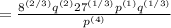`=(8^((2/3))q^((2))27^((1/3))p^((1))q^((1/3)))/(p^((4)))` Combine the like terms in the numerator with the base "q"

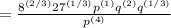`=(8^((2/3))27^((1/3))p^((1))q^((2))q^((1/3)))/(p^((4)))` Rearranged for you to see the like terms

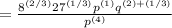`=(8^((2/3))27^((1/3))p^((1))q^((2)+(1/3)))/(p^((4)))` Multiplying exponents with same base

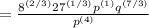`=(8^((2/3))27^((1/3))p^((1))q^((7/3)))/(p^((4)))` 2 + 1/3 = 7/3

`=\frac{\sqrt[3]{8^(2)}\sqrt[3]{27}p\sqrt[3]{q^(7)}}{p^(4)}` Fractional exponents as radical form

`=\frac{(\sqrt[3]{64})(3)(p)(q^{(7)/(3)})}{p^(4)}` Simplified cubes. Wrote brackets to lessen confusion. Notice the radical of a variable can't be simplified.

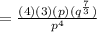`=\frac{(4)(3)(p)(q^{(7)/(3)})}{p^(4)}` Multiply 4 and 3

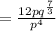`=\frac{12pq^{(7)/(3)}}{p^(4)}` Dividing exponents with same base

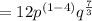`=12p^((1-4))q^{(7)/(3)}` Subtract the exponent of 'p'

`=12p^((-3))q^{(7)/(3)}` Negative exponent rule

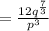`=\frac{12q^{(7)/(3)}}{p^(3)}` Final answer

Here is a version in pen if the steps are hard to see.