I don't have the time to sort them out for you, sadly, but, I can provide you with some steps for each.
1) That can only be solved with the Pythagorean theorem :
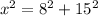
2) That also looks like it can be simplified with the Pythagorean theorem.
3) The unknown side with the "\" on it is equal to
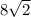
then it can be simplified massively with the Pythagorean theorem.
4) Since that triangle's total is 180°, and since we know that one side is 90°, the other two (assuming they're equal) have to be 45°, respectively. Knowing that you can find

then, all you have to do is find x (see below for more details)
5) to find x, you can first find
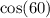
and then find x: (done similarly with triangle 4)
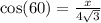
Just gonna leave the rest for you. Have a nice day!