Question

A horizontal 745 N merry-go-round of radius

1.45 m is started from rest by a constant
horizontal force of 56.3 N applied tangentially
to the merry-go-round.
Find the kinetic energy of the merry-goround after 3.62 s. The acceleration of gravity
is 9.8 m/s^2
Assume the merry-go-round is a solid cylinder.
Answer in units of J.

Answer 1

The kinetic energy of the merry-goround after 3.62 s is 544J

Step-by-step explanation:

Given :

Weight w = 745 N

Radius r = 1.45 m

Force = 56.3 N

To Find:

The kinetic energy of the merry-go round after 3.62 = ?

Solution:

Step 1: Finding the Mass of merry-go-round

`m = ( weight)/(g)`

`m = (745)/(9.81 )`

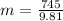
m = 76.02 kg

Step 2: Finding the Moment of Inertia of solid cylinder

Moment of Inertia of solid cylinder I =
`0.5 * m * r^2`

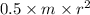
Substituting the values

Moment of Inertia of solid cylinder I

=>
`0.5 * 76.02 * (1.45)^2`

=>
`0.5 * 76.02* 2.1025`

=>
`79.91 kg.m^2`

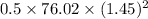
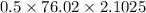
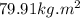
Step 3: Finding the Torque applied T

Torque applied T =
`F * r`

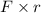
Substituting the values

T =
`56.3 * 1.45`

T = 81.635 N.m

Step 4: Finding the Angular acceleration

Angular acceleration ,
`\alpha = (Torque)/(Inertia)`

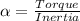
Substituting the values,

`\alpha = (81.635)/(79.91)`

`\alpha = 1.021 rad/s^2`

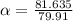
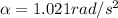
Step 4: Finding the Final angular velocity

Final angular velocity ,
`\omega = \alpha * t`

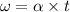
Substituting the values,

`\omega = 1.021 * 3.62`

`\omega = 3.69 rad/s`

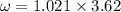
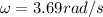
Now KE (100% rotational) after 3.62s is:

KE =
`0.5 * I * \omega^2`

KE =
`0.5 * 79.91 * 3.69^2`

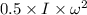
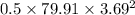
KE = 544J