Answer:
radius = 7 units
Explanation:
We are given the equation;
x² - 10x + y² - 10y = -1
We are required to determine the radius of the circle;
We are going to use completing square method to solve for the radius and the center of the circle.
First we make sure the coefficient of x² and y² is 1
x² - 10x + y² - 10y = -1
Then we add the square of half the coefficient of x and y on both sides of the equation;
That is;
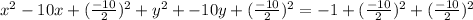
Simplifying the equation, we get;

Thus;
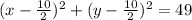
That is;
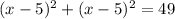
The equation of a circle is written in the form of;
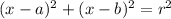
Then (a, b) is the center and r is the radius.
Therefore;
In our case;
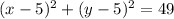
Then, center = ( 5, 5)
radius = √49
= 7 units