Question

Z=a/b+c/d solve for A

Answer 1

Answer:
`a=(b(zd-c))/(d)`

Explanation:

Having the following equation given in the exercise:

`z=(a)/(b)+(c)/(d)`

You can solve for "a" following this procedure:

1. You can apply the Subtraction property of equality and subtract
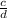`(c)/(d)` from both sides of the equation:

`z-((c)/(d))=(a)/(b)+(c)/(d)-((c)/(d))\\\\z-(c)/(d)=(a)/(b)`

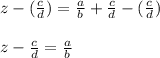
2. Now you must subtract the terms on the left side of the equation. Notice that the Least Common Denominator is "d". Then:

`(zd-c)/(d)=(a)/(b)`

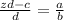
3. Finally, you can apply the Multiplication property of equality and multiply both sides of the equation by "b". So, you get:

`(b)((zd-c)/(d))=((a)/(b))(b)\\\\a=(b(zd-c))/(d)`