Question

Find the coordinates of the midpoint MM of ST. Then find the distance between points SS and TT. Round the distance to the nearest tenth. S(−2, 4) and T(3, 9)

Answer 1

The midpoint is
`((1)/(2), (13)/(2))`

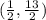
The distance between points S and T is 7.1 units

Solution:

Given points are S(−2, 4) and T(3, 9)

Find the coordinates of the midpoint of ST

The midpoint is given as:

`m(x, y)=\left((x_(1)+x_(2))/(2), (y_(1)+y_(2))/(2)\right)`

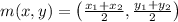
Here in this sum,

`(x_1, y_1) = (-2, 4)\\\\(x_2, y_2) = (3, 9)`

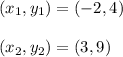
Substituting the values, we get

`m(x, y)=\left((-2+3)/(2), (4+9)/(2)\right)\\\\m(x, y)=\left((1)/(2), (13)/(2))`

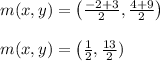
Thus the midpoint is
`((1)/(2), (13)/(2))`

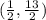
Find the distance between points

The distance is given by formula:

`d=\sqrt{\left(x_(2)-x_(1)\right)^(2)+\left(y_(2)-y_(1)\right)^(2)}`

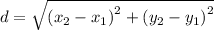
Here in this sum,

`(x_1, y_1) = (-2, 4)\\\\(x_2, y_2) = (3, 9)`

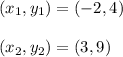
Substituting the values, we get

`\begin{aligned}&d=\sqrt{(3-(-2))^(2)+(9-4)^(2)}\\\\&d=\sqrt{5^(2)+5^(2)}\\\\&d=√(25+25)\\\\&d=√(50)=7.071 \approx 7.1\end{aligned}`

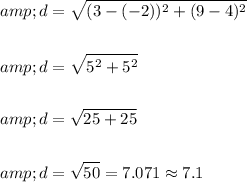
Thus the distance between points S and T is 7.1 units