Meteorite’s distance from the sun is
 kilometers
kilometers
Solution:
Given that,
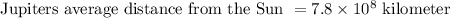
Also, given that,
The ratio comparing Jupiter’s distance from the Sun to a meteorite’s distance from the sun is

Which means,

Substitute the given value in above fraction,
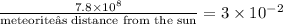
Solve for meteorite’s distance from the sun

Thus, meteorite’s distance from the sun is
 kilometers
kilometers