Answer:
The three points for the line y = -6x + 12 ...Red color line
point A( x₁ , y₁) ≡ ( 0 , 12) (blue color point on the graph)
point B( x₂ , y₂) ≡ (2 , 0) (green color point on the graph)
point C(x₃ , y₃ ) ≡ (1 , 6) (purple color point on the graph)
The Graph is attached below.
Step-by-step explanation:
Given:
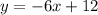........... equation of a line
Let the points be point A, point B, and point C
To Find:
point A( x₁ , y₁) ≡ ?
point B( x₂ , y₂) ≡ ?
point C(x₃ , y₃ ) ≡ ?
Solution:
For Drawing a graph we require minimum two points but we will have here three points.
For point A( x₁ , y₁)
Put x = 0 in the given equation we get
y = 0 + 12
y = 12
∴ point A( x₁ , y₁) ≡ ( 0 , 12)
For point B( x₂ , y₂)
Put y= 0 in the given equation we get
0 = -6x + 12
6x = 12
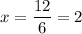
∴ point B( x₂ , y₂) ≡ (2 , 0)
For point C(x₃ , y₃ )
Put x = 1 in the given equation we get
y = -6 × 1 + 12
y = 6
∴ point C(x₃ , y₃ )≡ (1 , 6)
Therefore,
The three points for the line -2y = -x + 8 are
point A( x₁ , y₁) ≡ ( 0 , 12) (blue color point on the graph)
point B( x₂ , y₂) ≡ (2 , 0) (green color point on the graph)
point C(x₃ , y₃ ) ≡ (1 , 6) (purple color point on the graph)
The Graph is attached below..