Answer:
100 students play only basketball.
Explanation:
We are given the following information in the question:
Total number of students in school = 240
Number of students that play soccer =
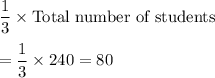
n(S) =80
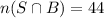
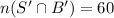
Formula:
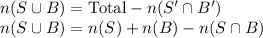
Putting the values, we get,
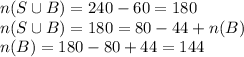
Thus, 144 students play basketball.
Out of these 144, 44 plays soccer as well.
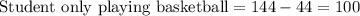
Thus, 100 students play only basketball and not soccer.