Question

Find, correct to the nearest degree, the three angles of the triangle with the given vertices.

A(1, 0, −1), B(5, −3, 0), C(1, 5, 2)

∠CAB =

∠ABC =
∠BCA =

Answer 1

angle CAB = 113.8 degree

angle ABC = 35.6 degree

angle BCA = 30.6 degree

Explanation:

Given data:

A(1, 0, −1),

B(5, −3, 0),

C(1, 5, 2)

calculate the length of side by using the distance formula

so

AB = (5,-3,0) - (1,0,-1) = (4,-3,1)

AC= (1,5,2) - (1,0,-1) = (0,5,3)

|AB|

|AC| =
`\sqrt {(0 + 5^2+3^2)} = √(34)`

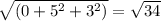
From following formula, calculate the angle between the two side i.e Ab and AC

AB.AC = |AB|*|AC| cos ∠CAB

(4,-3,1).(0,5,3)

4*0 -3*5 +1*3

-12 =

cos ∠CAB = - 0.404

angle CAB = 113.8 degree

BA =B- A = (1,0,-1) - (5,-3,0) = (-4,3,-1)

BC = (1,5,2)-(5,-3,0) = (-4,8,2)

|BA| = \sqrt{(26)}

|BC|
`= \sqrt {(4^2 + 8^2 + 2^2)} = √((84))`

BA.BC = |BA|*|BC|* cosABC

(-4,3,-1).(-4,8,2) =
`√((26)) * √((84)) *cosABC`

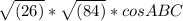
16+24-2

cos ∠ABC = 0.813

angle ABC = 35.6 degree

we know sum of three angle in a traingle is 180 degree hence

sum of all three angle = 180

angle BCA + 35.6 + 113.8 = 180

angle BCA = 30.6 degree