Answer: 700 (choice C)
======================================================
Step-by-step explanation:
At 99% confidence, the z critical value is roughly z = 2.576 which is found using a Z table.
We're given that
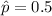 as the sample proportion and E = 0.05 is the desired error.
as the sample proportion and E = 0.05 is the desired error.
The min sample size n is:

Always round up to the nearest integer.
Unfortunately n = 664 isn't one of the answer choices. The next closest value is 700. It appears that your teacher wants to know a valid sample size that is the smallest of the answer choices, not necessarily the smallest ever possible.