Question

Solve triangles using the law of sines.

Answer 1

Measure of angle A

Explanation:

Answer 2

The measure of angle B is
`m \angle B=45`°

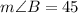Explanation:

Using law of sines ∠B can be found using,

`(\sin B)/(b)=(\sin C)/(c)`

where b,c denotes the side and B,C denotes the angle.

Also, it is given that
`b=10`,
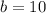`c=11` and ∠C=51°.

To find ∠B, let us substitute the values in this formula, we get,

`(\sin B)/(10)=(\sin 51^(\circ))/(11)`

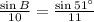
Multiplying both sides by 10, we get,

`\begin{aligned}\sin B &=(10)/(11) \sin 51^(\circ) \\&=(10)/(11)(0.7771) \\&=(7.771)/(11) \\\sin B &=0.7065\end{aligned}\\`

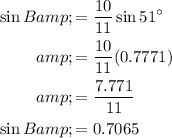
Taking
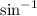`\sin ^(-1)` on both sides,

`\begin{aligned}&B=\sin ^(-1)(0.7065)\\&B=44.95^(\circ)\end{aligned}`

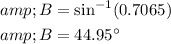
Rounding it off to the nearest degree,we get,

`m \angle B=45`

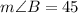
Thus, the measure of angle B is
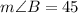`m \angle B=45`°