Question

A=5i+4j-6k ,b=-2i+2j+3k ,c=4i+3j+2k. find the vector perpendicular to a and c​

Answer 1

Step-by-step explanation:

You can use the cross product. Let the vector that perpendicular to a and c is
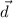`\vec{d}`, so:

`\vec{d}=\vec{a}*\vec{c}=\left|\left[\begin{array}{ccc}\hat{i}&\hat{j}&\hat{k}\\5&4&-6\\4&3&2\end{array}\right] \right|=(8+18)\hat{i}-\hat{j}(10+24)+\hat{k}(15-16)=26\hat{i}-34\hat{j}-\hat{k}`

To check that c is perpendicular with a and b, do the dot product between c and a and also c and b and if the result is zero, you're true.

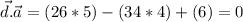`\vec{d}.\vec{a}=(26*5)-(34*4)+(6)=0` (c perpendicular to a)

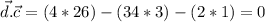`\vec{d}.\vec{c}=(4*26)-(34*3)-(2*1)=0` (d perpendicular to c)