Answer:
Step-by-step explanation:
You can use the cross product. Let the vector that perpendicular to a and c is
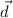 , so:
, so:
![\vec{d}=\vec{a}*\vec{c}=\left|\left[\begin{array}{ccc}\hat{i}&\hat{j}&\hat{k}\\5&4&-6\\4&3&2\end{array}\right] \right|=(8+18)\hat{i}-\hat{j}(10+24)+\hat{k}(15-16)=26\hat{i}-34\hat{j}-\hat{k}](https://img.qammunity.org/qa-images/2023/formulas/physics/college/ohxka4jobzg88z1z9mtm.png)
To check that c is perpendicular with a and b, do the dot product between c and a and also c and b and if the result is zero, you're true.
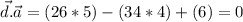 (c perpendicular to a)
(c perpendicular to a)
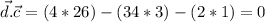 (d perpendicular to c)
(d perpendicular to c)