Population after 5 years = 534
Solution:
Given population, P = 690
Rate decrease, R = 5%
Number of years, n = 5
If the population decrease constantly R% , then the population after n years is
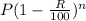
Substitute the given values in the above formula.
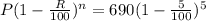
Cross multiply 1 and 100 to get the same denominator.

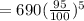
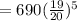
= 533.90
= 534
Hence the population after 5 years is 534.