Question

A college’s data about the incoming freshmen indicates that the mean of their high school GPAs was 3.4, with a standard deviation of 0.35; the distribution was roughly mound-shaped and only slightly skewed. The students are randomly assigned to freshman writing seminars in groups of 25. What might the mean GPA of one of these seminar groups be? Describe the appropriate sampling distribution model—shape, center, and spread— with attention to assumptions and conditions. Make a sketch using the 68–95–99.7 Rule.

Answer 1

Explanation:

u = 3.4

stdev = 0.35

n = 25

E = u = 3.4

SD =
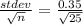`(stdev)/(√(n) ) =(0.35)/(√(25) )` = 0.07

The calculation of the 68% population covers with 1 standard deviation is as follows:

u - SD = 3.4 - 0.07 = 3.33

u + SD = 3.4 + 0.07 = 3.47

Range = (3.33, 3.47)

The calculation of the 95% population covers within 2 standard deviations is as follows:

u - 2SD = 3.4 - 2(0.07) = 3.26

u + 2SD = 3.4 + 2(0.07) = 3.54

Range = (3.26, 3.54)

The calculation of the 99.7% population covers within 3 standard deviations is as follows:

u - 3SD = 3.4 - 3(0.07) = 3.19

u + 3SD = 3.4 + 3(0.07) = 3.61

Range = (3.19, 3.61)

From the information, observe that the shape of the distribution is symmetrical.

Therefore, the graph is as shows the attached image.

This shows that approximately:

68% of the observations will have mean between 3.33 and 3.47

95% of the observations will have mean between 3.26 and 3.54

99.7% of the observations will have mean between 3.19 and 3.61