Question

To get up on the roof, a person (mass 92.0 kg) places a 5.60 m aluminum ladder (mass 14.0 kg) against the house on a concrete pad with the base of the ladder 2.00 m from the house. The ladder rests against a plastic rain gutter, which we can assume to be frictionless. The center of mass of the ladder is 2 m from the bottom. The person is standing 3 m from the bottom. What are the magnitudes (in N) of the forces on the ladder at the top and bottom?

Answer 1

Down

F1ₓ = 219.6N

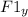`F1_(y)` = 1038.8 N

Top

F2ₓ = 219.6 N

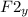`F2_(y)` = 0

Step-by-step explanation:

For this exercise we must make a free body diagram of the ladder, see attached, then use the balance equations on each axis

Transnational Balance

X axis

F1ₓ -F2ₓ = 0

F1ₓ = F2ₓ

Y Axis

`F1_(y)` -
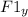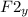`F2_(y)` - W - W_man = 0 (1)

Rotational balance

The reference system is placed at the bottom of the stairs and we can turn the anti-clockwise direction of rotation as positive

F2ₓ y -
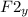`F2_(y)` x - W x - W_man x_man = 0

Let us write the data they give, the masses of the ladder (m = 14.0 kg), the mass of man (m_man = 92 kg), the center of mass of the ladder that is 2m from the bottom (the height) and the position of the man which is 3 m high

Let's look with trigonometry for distances

The angle of the stairs is

cos θ = x / L

θ = cos⁻¹ x / L

θ = cos⁻¹ 2 / 5.6

θ = 69⁰

Height y

tan 69 = y / x

y = x tan 69

y = 2 tan 69

y = 5.21 m

Distance x

tan 69 = 2 / x

x = 2 / tan 69

x = 0.7677 m

The distance x_man

x_man = 3 / tan 69

x_man = 1,152 m

They indicate that between the scalars and the support there is no friction so the vertical force at the top is zero

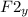`F2_(y)` = 0

Let's replace in the translational equilibrium equation

F2ₓ y -
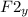`F2_(y)` x - W x - W_man x_man = 0

F2ₓ 5.21 -0 - 14.0 9.8 0.7677 - 92.0 9.8 1,152 = 0

F2ₓ = 1143.97 / 5.21

F2ₓ = 219.6 N

We use equation 1

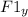`F1_(y)` + 0 - W - W_man = 0

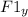`F1_(y)` = W + W_man

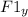`F1_(y)` = (m + m_man) g

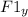`F1_(y)` = (14 +92) 9.8

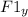`F1_(y)` = 1038.8 N

We can write the force on each part of the ladder

Down

F1ₓ = 219.6N

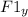`F1_(y)` = 1038.8 N

Top

F2ₓ = 219.6 N

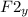`F2_(y)` = 0