Answer:
The length of the side of an equilateral traingle
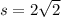 inches
inches
Explanation:
Given that the area of an equilateral triangle is given by
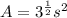
It can be written as
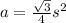 Square inches (1)
Square inches (1)
To find the length of the side s os an equilateral triangle
Given that area of an equilateral triangle is
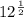 square inches
square inches
It can be written as
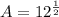
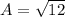 square inches
square inches
It can be written as
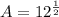
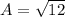 square inches (2)
square inches (2)
Now comparing equations (1) and (2) we get

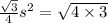
Dividing by
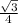 on both sides we get
on both sides we get

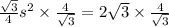
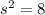
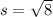
Therefore
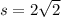 inches
inches
Therefore the length of the side of an equilateral traingle
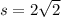 inches
inches