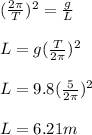Answer:

Step-by-step explanation:
For the simple pendulum problem we need to remember that:
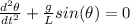 ,
,
where
 is the angular position, t is time, g is the gravity, and L is the length of the pendulum. We also need to remember that there is a relationship between the angular frequency and the length of the pendulum:
is the angular position, t is time, g is the gravity, and L is the length of the pendulum. We also need to remember that there is a relationship between the angular frequency and the length of the pendulum:
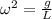 ,
,
where
 is the angular frequency.
is the angular frequency.
There is also an equation that relates the oscillation period and the angular frequeny:
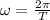 ,
,
where T is the oscillation period. Now, we can easily solve for L: