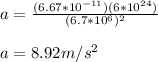Answer:

Step-by-step explanation:
For this problem, we need to make use of Newton's law of universal gravitation. This law states that two objects attract each other with a force that is inversely proportional to the square of the distance of their centers of mass and directly proportional to the product of their masses. We can write this as:
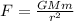
where F is the attractive force, G is the gravitational constant, r is the distance between their centers of mass, and M and m are the masses of the objects.
From here we will let M be the mass of the earth, and m the mass columbia. From Newton's second law, we know that the gravitational force exerted to columbia due to the earth can be written as
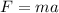 ,
,
here, making a substitution we get
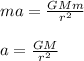
The distance between columbia and the earth's center is
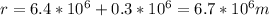 .
.
Now, computing the acceleration: