Question

Suppose that a company ships packages that are variable in weight, with an average weight of 15 lb and a standard deviation of 10. Assuming that the packages come from a large number of different customers so that it is reasonable to model their weights as independent random variables, find the probability that 100 packages will have a total weight exceeding 1700 lb.

Answer 1

ANSWER= 0.9772

STEP-BY-STEP EXPLANATION:

We are assuming that there is an underlying distribution of package weights,even though we don´t speciify the shape of that distribution.

Letting
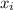`x_(i)` denote the ith package weight and S=
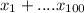`x_(1) +....x_(100)` we are trying to find P(S ≤ 1700)

We know that the distribution of S is approximately normal with mean nцХ and variance по²Х

S≈N( 100 * 15, 100 * 10² ) = N (1500.10000) (note that they gave us the standar deviation aove; variances add, so we need to square this). Finally,

P(S ≤ 1700) = P (
`(S-1500)/(√(10000) )` ≤
`(1700 - 1500)/(√(10000) )`)

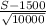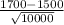≈P (Z≤2) = 0.9772