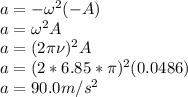Answer:
A)
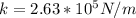 .
.
B)

C)
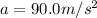
Step-by-step explanation:
This problem is a simple harmonic motion problem. The equation of motion for the SHM is:
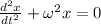 ,
,
where x is the displacement of the mass about its point of equilibrium, t is time, and
 is the angular frequency.
is the angular frequency.
A)
First, we need to remember that
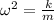 ,
,
where k is the spring constant, and m is the mass.
From here we can simply solve for k, so
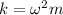 .
.
Now, we need to make use of an equation that relates the frequency and angular frequency. The equetion is
 ,
,
where
 is the frequency. This leads us to
is the frequency. This leads us to
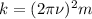 ,
,
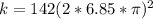 ,
,
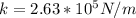 ,
,
B) In simple harmonic motion, the velocity behaves as follow:
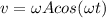 (this is obtained by solving the equation of motion of the mass for the displacement x and take the derivative),
(this is obtained by solving the equation of motion of the mass for the displacement x and take the derivative),
where A is the amplitude of the motion. Since we want the maximum value for the speed, we make
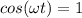 (this because cosine function goes from -1 to 1). With this, the maximum speed is simply
(this because cosine function goes from -1 to 1). With this, the maximum speed is simply
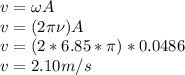
C) Here we are going to use the equation of motion of SHM
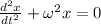 ,
,
we know that
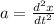 , where a is the acceleration,
, where a is the acceleration,

in this case, x goes from -A to A, so for a to be maximum we need that
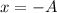 ,and we get
,and we get