Question

I need the last two

Answer 1

Part 5) Option b
`2x√(3)\ ft`

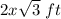
Part 6) Option d.
`4y\sqrt[3]{2}\ mm`

Explanation:

Part 5) we know that

The area of a square is equal to

`A=b^2`

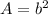
where

b is the length side of the square

we have

`A=12x^2\ ft^2`

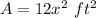
substitute

`12x^2=b^2`

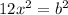
Solve for b

take square root both sides

`b=\sqrt{12x^(2)}`

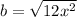
Remember that

`12=(2^2)(3)`

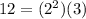
substitute

`b=\sqrt{(2^2)(3)x^(2)}`

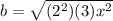
Applying property of exponents

`b=\sqrt{(2^2)(3)x^(2)}=[(2^2)(3)x^(2)]^{(1)/(2)}=[2^2x^2]^{(1)/(2)}3^{(1)/(2)}=2x√(3)\ ft`

Part 6) we know that

The volume of a cube is equal to

`V=b^3`

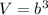
where

b is the length side of the cube

we have

`V=128y^3\ mm^3`

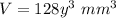
substitute

`128y^3=b^3`

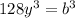
Solve for b

take cubic root both sides

`b=\sqrt[3]{128y^3}`

Remember that

`128=(2^7)=(2^6)(2)=(2^2)^3(2)`

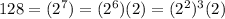
substitute

`b=\sqrt[3]{(2^2)^3(2)y^3}`

Applying property of exponents

`b=\sqrt[3]{(2^2)^3(2)y^3}=[(2^2)^3(2)y^3]^{(1)/(3)}=[(2^2)^3y^3]^{(1)/(3)}2^{(1)/(3)}=2^2y\sqrt[3]{2}=4y\sqrt[3]{2}\ mm`