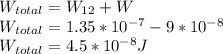Answer:
Step-by-step explanation:
Remember that electric potential can be written as:
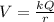 ,
,
Where V is the electric potential, k is Coulomb's constant, Q is a point charge, and r is the distance from the point charge. Also, we can write the electric potential as:
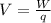 ,
,
where W is the work made to move a charge from infinitely far apart to a certain distance, and q the point charge were are moving.
From all this we can get an expression for the work:
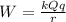
We are going to let
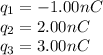
To take the first charge
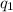 from infinitely far apart to one of the vertices of the triangle, since there is no electric field and charges, we make no work.
from infinitely far apart to one of the vertices of the triangle, since there is no electric field and charges, we make no work.
Next, we will move
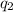 . Now,
. Now,
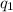 is a vertice of the triangle, and we want
is a vertice of the triangle, and we want
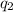 to be 20.cm apart from
to be 20.cm apart from
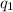 so the work we need to do is
so the work we need to do is
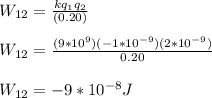
Now, we move the last point charge. Here, we need to take in account the electric potential due to
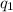 and
and
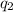 . So
. So
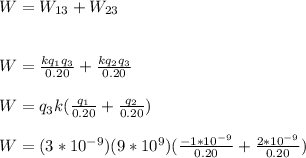
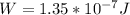
Now, the only thing left to do is to find the total work, this can be easily done by adding
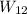 and
and
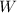 :
: