y = -x - 1 is the equation of the line that passes through (2,-3) and is perpendicular to y = x - 5
Solution:
Given that we have to write the equation of the line that passes through (2,-3) and is perpendicular to y = x - 5
The equation of line in slope intercept form is given as:
y = mx + c ------ eqn 1
Where, "m" is the slope of line and "c" is the y intercept
Given equation of line is:
y = x - 5
On comparing the above equation with eqn 1,
m = 1
We know that,
Product of slope of line and slope of line perpendicular to given line is equal to -1
Therefore,
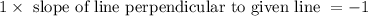
Slope of line perpendicular to given line = -1
Now we have to find the equation of line with slope -1 and passing through (2, -3)
Substitute m = -1 and (x, y) = (2, -3) in eqn 1
-3 = -1(2) + c
-3 = -2 + c
c = -3 + 2
c = -1
Substitute m = -1 and c = - 1 in eqn 1
y = -x - 1
Thus the equation of line is found