Question

F

(
x
)
=
−
x
2
+
6
x
+
13
f(x)=−x
2
+6x+13, determine the average rate of change of the function over the interval
−
1
≤
x
≤
5
−1≤x≤5.

Answer 1

The average rate of change of
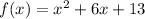`f(x) = x^2 +6x+13` is 12

The average rate of change of
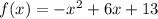`f(x) =- x^2 +6x+13` is 10

Explanation:

The average rate of change of f(x) over an interval between 2 points (a ,f(a)) and (b ,f(b)) is the slope of the secant line connecting the 2 points.

We can calculate the average rate of change between the 2 points by

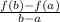`(f(b) - f(a))/(b -a)`-------------------(1)

(1) The average rate of change of the function
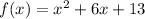`f(x) = x^2 +6x+13` over the interval 1 ≤ x ≤ 5

f(a) = f(1)

`f(1) = (1)^2 +6(1) + 13`

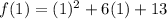
f(1) =1+6+13

f(a) = 20---------------------(2)

f(b) = f(5)

`f(5) = (5)^2 +6(5)+13`

f(5) = 25 +30 +13

f(5) = 68-----------------------(3)

The average rate of change between (1 ,20) and (5 ,68 ) is

Substituting eq(2) and(3) in (1)

=
`(f(5) - f(1))/(5-1)`

=
`(68 -20)/(5-1)`

=
`(48)/(4)`

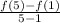
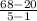
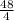
=12

This means that the average of all the slopes of lines tangent to the graph of f(x) between (1 ,20) and (5 ,68 ) is 12

(2) The average rate of change of the function
`f(x) = -x^2 +6x+13` over the interval -1 ≤ x ≤ 5

f(a) = f(-1)

`f(1) = (-1)^2 +6(-1) + 13`

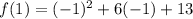
f(1) =1-6+13

f(1) = 8---------------------(4)

f(b) = f(5)

`f(5) = (5)^2 +6(5)+13`

f(5) = 25 +30 +13

f(5) = 68-----------------------(5)

The average rate of change between (-1 ,8) and (5 ,68 ) is

Equation (1) becomes

`(f(5) - f(-1))/(5-(-1))`

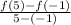
On substituting the values

=
`(68 - 8)/(5-(-1))`

=
`(60)/(5+1)`

=
`(60)/(6)`

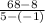
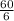
= 10

This means that the average of all the slopes of lines tangent to the graph of f(x) between (-1 ,8) and (5 ,68 ) is 10