Question

The probability that a professor arrives on time is 0.8 and the probability that a student arrives on time is 0.6. Assuming these events are independent: a) What is the probability that both the student and the professor are late? b) What is the probability that the student is late given that the professor is on time? c) Now assume the events are not independent. The probability that the professor is late given that the student is late is 0.4 i. What is the probability that at least one of them is on time?ii. What is the probability that they are both on time?

Answer 1

a)0.08 , b)0.4 , C) i)0.84 , ii)0.56

Explanation:

Given data

P(A) = professor arrives on time

P(A) = 0.8

P(B) = Student aarive on time

P(B) = 0.6

According to the question A & B are Independent

P(A∩B) = P(A) . P(B)

Therefore

`{A}'` &
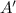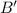`{B}'` is also independent

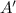`{A}'` = 1-0.8 = 0.2

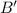`{B}'` = 1-0.6 = 0.4

part a)

Probability of both student and the professor are late

P(A'∩B') = P(A') . P(B') (only for independent cases)

= 0.2 x 0.4

= 0.08

Part b)

The probability that the student is late given that the professor is on time

`P((B')/(A))` =
`(P(B'\cap A))/(P(A))` =
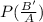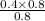`(0.4* 0.8)/(0.8)` = 0.4

Part c)

Assume the events are not independent

Given Data

P
`(\frac{{A}'}{{B}'})` = 0.4

=
`\frac{P({A}'\cap {B}')}{P({B}')}` = 0.4

`P`
`({A}'\cap {B}')` = 0.4 x P
`({B}')`

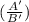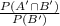= 0.4 x 0.4 = 0.16

`P({A}'\cap {B}')` = 0.16

i)

The probability that at least one of them is on time

`P(A\cup B)` = 1-
`P({A}'\cap {B}')`

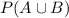= 1 - 0.16 = 0.84

ii)The probability that they are both on time

P
`(A\cap B)` = 1 -
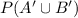`P({A}'\cup {B}')` = 1 -
`[P({A}')+P({B}') - P({A}'\cap {B}')]`

= 1 - [0.2+0.4-0.16] = 1-0.44 = 0.56