Question

A rectangle has width that is 6 meters less than the length. The area of the rectangle is 280 square meters. Find the dimensions.

Answer 1

Dimensions are length 20 meter and width 14 meter

Solution:

Let "a" be the length of rectangle

Let "b" be the width of rectangle

Given that,

A rectangle has width that is 6 meters less than the length

Width = length - 6

b = a - 6

The area of the rectangle is 280 square meters

The area of the rectangle is given by formula:

`Area = length * width`

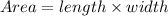
Substituting the values we get,

`Area = a * (a-6)\\\\280 = a^2-6a\\\\a^2-6a -280=0`

Solve the above equation by quadratic formula

`\mathrm{For\:a\:quadratic\:equation\:of\:the\:form\:}ax^2+bx+c=0\mathrm{\:the\:solutions\:are\:}\\\\\quad x_(1,\:2)=(-b\pm √(b^2-4ac))/(2a)`

`\mathrm{For\:}\quad a=1,\:b=-6,\:c=-280:\quad a_(1,\:2)=(-\left(-6\right)\pm √(\left(-6\right)^2-4\cdot \:1\left(-280\right)))/(2\cdot \:1)`

`a =(6 \pm √(36+1120))/(2)\\\\a = (6 \pm √(1156))/(2)\\\\a = (6 \pm 34)/(2)\\\\Thus\ we\ have\ two\ solutions\\\\a = (6+34)/(2) \text{ or } a = (6-34)/(2)\\\\a = 20 \text{ or } a = -14`

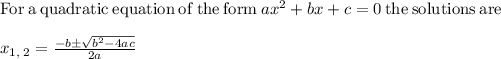
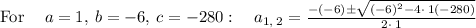
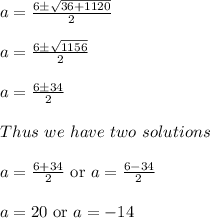
Since, length cannot be negative, ignore a = -14

Thus solution of length is a = 20

Therefore,

width = length - 6

width = 20 - 6 = 14

Thus dimensions are length 20 meter and width 14 meter