Question

Suppose quantity s is a length and quantity t is a time. Suppose the quantities vand aare defined by v = ds/dt and a = dv/dt. (a) What is the dimension of v? (b) What is the dimension of the quantity a?

What are the dimensions of (c)vdt, (d) a dt, and (e) da/dt?

Answer 1

Step-by-step explanation:

(a) Velocity is given by :

`v=(ds)/(dt)`

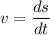
s is the length of the distance

t is the time

The dimension of v will be,
`[v]=[LT^-1]`

(b) The acceleration is given by :

`a=(dv)/(dt)`

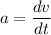
v is the velocity

t is the time

The dimension of a will be,
`[a]=[LT^(-2)]`

(c) Since,
`d=\int\limits{v{\cdot}dt} =[LT^(-1)][T]=[L]`

(d) Since,
`v=\int\limits{a{\cdot}dt} =[LT^(-2)][T]=[LT^(-1)]`

(e)

`(da)/(dt)=([LT^(-2)])/([T])`

`(da)/(dt)=[LT^(-3)]}`

Hence, this is the required solution.